Archives

  • 2018-07
  • 2018-10
  • 2018-11
  • 2019-04
  • 2019-05
  • 2019-06
  • 2019-07
  • 2019-08
  • 2019-09
  • 2019-10
  • 2019-11
  • 2019-12
  • 2020-01
  • 2020-02
  • 2020-03
  • 2020-04
  • 2020-05
  • 2020-06
  • 2020-07
  • 2020-08
  • 2020-09
  • 2020-10
  • 2020-11
  • 2020-12
  • 2021-01
  • 2021-02
  • 2021-03
  • 2021-04
  • 2021-05
  • 2021-06
  • 2021-07
  • 2021-08
  • 2021-09
  • 2021-10
  • 2021-11
  • 2021-12
  • 2022-01
  • 2022-02
  • 2022-03
  • 2022-04
  • 2022-05
  • 2022-06
  • 2022-07
  • 2022-08
  • 2022-09
  • 2022-10
  • 2022-11
  • 2022-12
  • 2023-01
  • 2023-02
  • 2023-03
  • 2023-04
  • 2023-05
  • 2023-06
  • 2023-08
  • 2023-09
  • 2023-10
  • 2023-11
  • 2023-12
  • 2024-01
  • 2024-02
  • 2024-03
  • 2024-04

    • Note that for correct simulation of mechanical

    2018-11-03

    Note that, for correct simulation of mechanical response of such complex heterogeneous materials, it is necessary to take into account main features of their internal structure. For this purpose, a two-dimensional structural and rheological model of MCC in the framework of MCA method was proposed in the paper. In this model, each of the composite constituents is simulated by an ensemble of movable cellular automata with appropriate rheological parameters (thus the cellular automaton simulates a domain/fragment of an inclusion, or a binder, or an interface zone). As an example of MCA-based structural model, Fig. 6(a) shows the structure of an idealized metal–ceramic composite with TiC particles having an equiaxed shape and the average size DTiC of 3 μm. The components of the metal–ceramic composites have very different rheological characteristics (in case of considered composite these are elastic-brittle high-strength TiC inclusions and elastic–plastic NiCr binder). For correct modeling of deformation and fracture of such complex systems, the mathematical formalism of constructing many-particle interaction forces for cellular automata (discrete elements) with different rheological characteristics was developed [27,33,41]. In the following calculations, the plane stress approximation is used. The elastic constants and diagram of uniaxial loading of the material are used as the input parameters of the model to characterize the inter-element interaction (the mechanical response function of movable cellular automaton). The response function of automaton modeling NiCr is considered as a stress–strain diagram with linear hardening (Curve 1 in Fig. 6(b)). This diagram is an approximation of the experimental diagram of uniaxial promethazine hydrochloride of macroscopic samples of the alloy. The mechanical properties of the automata that simulate the high-strength brittle inclusions meet the real properties of TiC particles in the ceramic phase (polycrystalline particles, Curve 2 in Fig. 6(b)). Two-parameter Drucker–Prager fracture criterion in Eq. (17) is used to describe the fractures of metallic binder and carbide particles in the developed model [27,33,41]. Thus, in this work, the strength characteristics of the composite material are determined by the tensile (σt) and compressive (σc) strength of it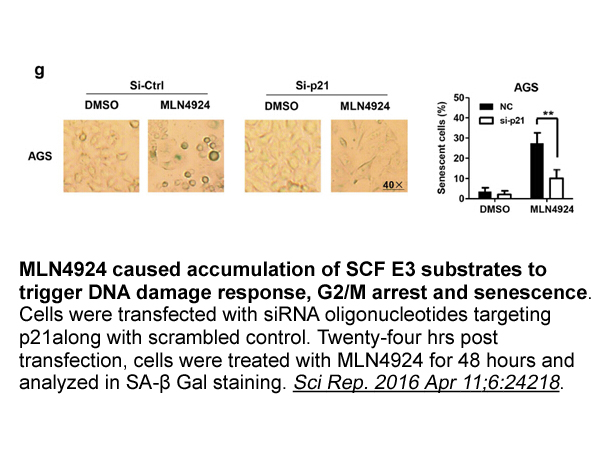s components. The developed model was used for investigating the influence of the main features of internal structure on the basic characteristics of mechanical behavior of the metal–ceramic composite. For this purpose, a three-point bending test [42,43] of the model samples of MCC was simulated. The structure of the model set-up is shown in Fig. 7. Dynamic loading of 20 μm cylindrical mandrel at constant velocity Vload = 0.5 m/s was applied to the sample of 24 × 130 μm in dimensions. The value of the maximal resistance of the sample to bending and the corresponding displacement of the mandrel, as well as the dynamics and pattern of the sample fracture were analyzed. It is well known that the strength of reinforcing particles largely determines the integral characteristics of the composite. Cracking of particles, containing significant (large) internal defects and damages, leads to the nucleation of internal cracks at lower applied loads and furthermore accelerates the crack growth. As a consequence, such integrated mechanical characteristics of the composite as strength and deformation ability could substantially reduce. Therefore, the influence of the strength of the TiC particles, which characterizes their initial defect structure or density of damages, on the integral mechanical response of the material was analyzed in the paper. It should be noted that the compressive and tensile strengths of brittle materials can differ by an order of magnitude (σc >> σt). The physical reason of this difference is that the damages, which initially exist and emerge in the process of loading, function in different ways under the action of compressive and tensile stresses. In conditions of compression (including uniaxial), the surfaces of a damage could occlude. This leads to their relative resistance to compression and shear (because of adhesion and dry friction of the damage surfaces). A spatial diversity of the damage surfaces occurs under the conditions of tension. Since the edges of damages are the stress concentrators, the absence of plastic deformation provides the conditions for the fast growing of damages and cracks. Thus, the key strength characteristic, which determines the integral strength of TiC particles in the composite, is its tensile strength (σt). In the paper, the value of σt varied from 700 MPa that corresponds to the tensile strength of the metallic binder NiCr to 2000 MPa. The choice of this interval is determined by the known fact that the tensile strength of real samples with typical dimensions of 1 ÷ 10 microns are generally 15 ÷ 50 times less than the theoretical strength of material (44 ÷ 88 GPa for TiC in the case of absence of large damages). The value of σc for TiC particles in all calculations was equal to 10,000 MPa.